При обучении одного потока используются процедуры подбора шага оптимизации - Increase (поиск шага в сторону возрастания, блок-схему см. на рис. 6), Decrease (поиск шага в сторону убывания, блок-схему см. на рис. 7) и Parabola (поиск оптимального шага по формулам параболического поиска блок-схему см. на рис. 8).

В процедурах используются следующие обозначения:

H( .) - функция оценки сети, накопленная по всему задачнику;

h1, h2, h3 - различные значения величины шага оптимизации, используемые при ее подборе;

W - величина шага в вершину параболы, проходящей через точки (h1, H1), (h2, H2), ( h3, H3). Вычисляется по формуле:

H1, H2, H3 - значения функции ошибки, соответствующие смещению обучаемых параметров по направлению градиента на величину шага h1, h2 è h3.

Условие выпуклости комбинации h1,2,3, H1,2,3 определяется формулой

Если выражение истинно, то условие выпуклости выполнено.

Теперь, рассмотрев алгоритмы обучения сети, перейдем к описанию компонентов, структуры и функционирования сети.

4.5 Оценка информационной емкости нейронной сети при помощи выборочной константы Липшица

Условие остановки процесса пошагового исчерпания ошибки может основываться также на оценке полноты функции, заданной нейронной сетью. В случае, если число элементов сети задано (для каждого шага наращивания «поточной» это так) и значения ее параметров ограничены на определенном интервале (это условие выполняется наложением ограничений на параметры сети), данное условие можно сформулировать с использованием константы Липшица. Константа Липшица вектор-функции в области D определяется как . 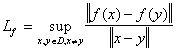Верхняя грань может быть вычислена по области определения D. В качестве оценки расстояния используется евклидова норма.

Для суперпозиции вектор-функций .

Для линейной комбинации функций оценка константы Липшица .

Константа Липшица для адаптивного сумматора, работающего по формуле имеет вид .

Тогда для стандартной комбинации, состоящей из матрицы входных синапсов, сумматора и преобразователя - нейрона с гладкой функцией активации .

Для прямой суммы вектор-функций константа Липшица может быть оценена как .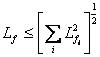

Таким образом, для слоя нейронов с подбираемыми преобразователями 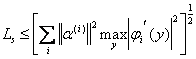, где - вектор весов синапсов, приходящих на входной сумматор i-го нейрона, а - функция i-го преобразователя.